Gastando salário com ações da empresa

Um notícia de setembro, mas que é interessante: O CEO do Deutsche vai gastar parte do seu salário para comprar ações do próprio banco.

Segundo o Financial Times (via Valor), Christian Sewing está comprando ações do próprio banco. O Deutsche Bank tem passado por uma série de problemas, que inclui denúncias de corrupção e reestruturação com fechamento de postos de trabalho. O executivo anunciou que irá comprar ações no equivalente a 15% do salário líquido, até o final de 2022. Isto corresponde a 850 mil euros. Além dele, o presidente do conselho de administração investiu 1 milhão de euros.

Por um lado, isto pode demonstrar uma sinalização para os investidores, em um momento que as ações estão em um patamar mínimo. No momento do anúncio, a ação tinha um valor de 8,33, sendo o máximo - nos últimos cinco anos - de 35 US$ no passado distante:

Rir é o melhor remédio

Dez razões para continuar blogando

1. tenho algo interessante para dizer para as pessoas
2. é uma forma de reter um conhecimento importante
3. as pessoas reconhecem o esforço
4. conhecemos pessoas
5. força a reflexão sobre diversos temas
6. aprendemos muito com aquilo que postamos
7. tenho liberdade para escolher temas das postagens
8. serve como material para escritos futuros
9. ajuda na exposição de ideias
10. é uma forma de ensinar

Mais ideias? (11. Posso contar com a ajuda dos leitores)

Dez razões para deletar o blog

1. estamos perdendo o livre-arbítrio
2. é uma maneira mais bem direcionada de resistir à insanidade de nossos tempos
3. está me fazendo um idiota
4. está minando a verdade
5. está fazendo sem sentido o que você posta
6. está destruindo a capacidade de empatia
7. está me deixando infeliz
8. não tenho remuneração
9. está tornando impossível falar seriamente de política
10. evito levar em consideração meus sentimentos

Livremente adaptado

Computação e Teoremas da Matemática

Talvez por influência de um doutorando em matemática, que está trabalhando com provador de teoremas computacionais, achei interessante o texto abaixo:

Há uma infecção de software na matemática pura. Alguns dos intelectuais peso-pesados do campo, renomados por sua autoconfiança, estão começando a se voltar para software para ajudá-los a entender e verificar provas.

Kevin Buzzard, um teórico dos números e professor de matemática pura do Imperial College London, acredita que agora é a hora de criar uma área na matemática dedicada a provas computadorizadas. As maiores provas para teoremas se tornaram tão complexas que praticamente nenhum humano na Terra pode entender todos os seus detalhes, quanto mais verificá-las. Ele teme que muitas provas consideradas verdade estão erradas. É preciso ajuda de fora.

O que é uma prova? Uma prova é uma demonstração da verdade num teorema. Ao provar tais teoremas, e ao aprender novas técnicas para esse processo, as pessoas evoluem o conhecimento de matemática, que depois é filtrado em outros campos.

Para criar uma prova, comece com algumas definições, ou axiomas. Por exemplo, defina um conjunto de números como números inteiros, todos os números de negativo infinito para positivo infinito. Escreva esse conjunto como: … , -2, -1, 0, 1, 2, … Em seguida, exponha um teorema, por exemplo, que não há um número inteiro maior. A prova então consiste no raciocínio lógico que mostra que o teorema é verdadeiro ou falso - neste caso, verdadeiro. Os passos lógicos na prova dependem de outras verdades anteriores, que já foram aceitas e provadas. Por exemplo, que o número 1 é menor que 2.


Novas provas de matemáticos profissionais tendem a depender de toda uma gama de resultados anteriores que já foram publicados e entendidos. Mas Buzzard diz que há muitos casos onde essas provas anteriores usadas para construir novas provas são claramente não entendidas. Por exemplo, há artigos notáveis que citam abertamente trabalhos que não foram publicados. Isso preocupa Buzzard.

“Agora estou preocupado pensando que toda a matemática publicada está errada, porque os matemáticos não estão conferindo os detalhes, e já vi eles errarem antes”, contou Buzzard ao Motherboard enquanto participava da décima conferência Interactive Theorem Proving em Portland, Oregon, onde ele deu uma palestra.

“Acho que há uma chance acima de zero de que alguns dos nossos castelos tenham sido construídos na areia”, Buzzard escreveu numa apresentação de slides. “Mas acho que é pequena.”


Novas teorias matemáticas deveriam ser provadas do zero. Cada passo precisa ser conferido, ou pelo menos esse é o raciocínio. Por outro lado, há especialistas sêniores e mais antigos da comunidade de matemática que fornecem um guia de testemunho confiável para o que é verdade e o que não é. Se um desses matemáticos mais velhos cita um artigo e o usa em seu trabalho, então o artigo provavelmente não precisaria ser conferido, segundo esse pensamento.

Buzzard aponta que essa matemática moderna se tornou dependente demais dos antigos porque os resultados se tornaram muito complexos. Uma nova prova pode citar outros 20 artigos, e só um desses 20 pode envolver mil páginas de raciocínio denso. Se um matemático respeitado cita o artigo de mil páginas, ou constrói sua teoria sobre ele, então muitos outros matemáticos podem supor que esse artigo de mil páginas (e a nova prova) é verdadeiro e não vão se dar ao trabalho de conferi-lo. Mas matemática deveria ser universalmente provável, não dependente de um punhado de especialistas.

Essa dependência excessiva dos matemáticos antigos leva a uma fragilidade na compreensão da verdade. Uma prova do Último Teorema de Fermat, proposto em 1637 e que já foi considerado pelo Guinness o “problema matemático mais difícil” do mundo, foi publicada nos anos 1990. Buzzard propõe que ninguém realmente a entende completamente, ou sabe se a prova é mesmo verdade.

“Acredito que nenhum humano, vivo ou morto, conhece todos os detalhes da prova do Último Teorema de Fermat. Mas a comunidade aceita a prova mesmo assim”, Buzzard escreveu em sua apresentação. Porque “os matemáticos antigos decretaram que a prova está certa”.

Alguns anos atrás, Buzzard assistiu palestras dos matemáticos sêniores Thomas Hales e Vladimir Voevodsky, que o apresentaram a um software de verificação de provas que estava se tornando muito bom. Com esse software, as provas podiam ser verificadas sistematicamente por um computador, as tirando das mãos dos matemáticos antigos e democratizando o status da verdade.

Quando Buzzard começou a usar o software de verificação de provas chamado Lean, ele ficou viciado. Não só o software permitia que ele verificasse provas além de qualquer dúvida, ele também o ajudava a pensar sobre matemática de um jeito claro e inconfundível.

“Percebi que computadores só aceitam inputs numa forma muito precisa, que é o meu jeito favorito de pensar em matemática”, disse Buzzard. “Me apaixonei pelo software, porque foi como encontrar uma alma gêmea. Descobri algo que pensava em matemática do mesmo jeito que eu.”

Para verificar sua prova, um usuário do Lean tem que formalizar a prova, ou a converter da linguagem humana para símbolos da linguagem de programação do Lean. O usuário também precisa formalizar quaisquer definições e provas subsidiárias de que o novo trabalho depende. E mesmo que esse processo de conversão seja trabalhoso, o Lean parece capaz de lidar com qualquer matemática que Buzzard joga nele, o que o distingue de outros programas assistentes de provas.

O Lean tem atraído interesse de uma comunidade crescente de matemáticos, particularmente na área de ensino. Jeremy Avigad é um professor da Universidade Carnegie Mellon especializado em teoria da prova. Tanto Avigad como Buzzard começaram a usar o Lean em aulas universitárias introdutórias de prova. O software verifica a veracidade de cada linha de uma prova e dá um feedback, o que é útil para os estudantes.

Apesar de Avigad estar empolgado com a comunidade que se interessou pelo Lean, ele alerta que a tecnologia ainda precisa de melhorias. Assistentes de provas exigem muito tempo para usar. “O campo existe há algumas décadas e as coisas estão melhorando, mas ainda não chegamos lá”, afirmou.


Se esses desafios puderem ser superados, Buzzard acredita que o software pode ter efeitos ainda mais amplos além de provas. Por exemplo, o problema da busca. Grandes quantidades de novos trabalhos são publicados todo ano, em grande velocidade, tornando a busca através dessas provas extremamente importante.

Hales e Buzzard apontaram que se todos os resumos de artigos fossem colocados no Lean, então qualquer matemático poderia consultar a base de dados desses resumos por um tema matemático preciso do Lean, e encontrar tudo que é sabido sobre ele. Até certo ponto, os cérebros inescrutáveis dos matemáticos antigos poderiam ser virados do avesso.

Cientistas da computação poderiam usar uma base de dados para treinar inteligências artificiais. Como os resultados dessa base de dados seriam definidos pela linguagem precisa do Lean, seria muito mais fácil para um programa aprender do que de resultados comparados escritos em inglês idiossincrático.

No final das contas, cientistas da computação poderia criar um provador geral de teoremas automatizado, um sistema de software que pode criar suas próprias provas e fazer sua própria matemática. Provadores automatizados dependem da mesma tecnologia do Lean para determinar se uma prova é verdadeira. O aumento da adoção do Lean pode se tornar um passo formativo importante para uma matemática automatizada no geral.

O Helix Center de Manhattan vai fazer uma mesa redonda de discussão sobre automação da matemática em 5 de outubro, transmitida ao vivo no YouTube e no site deles. Michael Harris, professor de matemática da Universidade de Columbia e colega de Buzzard, vai participar do fórum.

Harris teme que cientistas da computação e empresas de tecnologia que querem automatizar a matemática não compartilhem as mesmas motivações que os matemáticos. Cientistas da computação, por exemplo, querem usar a tecnologia por trás do Lean para se certificar de que programas não tenham bugs. Empresas querem lucro. Matemáticos como Buzzard só querem fazer matemática.

“Uma coisa que posso prever é que se pessoas realmente inteligentes como Thomas Hales e Buzzard continuarem a pensar nessa linha, então algo interessante vai sair disso; pode não ser uma IA, mas podem ser novos ramos da matemática ou novas maneiras de pensar”, imagina Harris.

Rir é o melhor remédio

Roubando um contador: Preciso de um recibo.

PhD, Doctor, Physician - Brooklyn Nine Nine - S05E14

Para quem assistiu/assiste Brooklyn Nine Nine. Ou para quem é doutor/doutorando - no sentido de fazer o doutorado - e não se conforma em ver um médico ser chamado de "doutor" (quanto mais um rábula).
 

Via aqui. (O autor do blog é chamado pelo NY Times de Mr, apesar de ser PhD; e médicos são chamados pelo jornal de Doctor, apesar de serem graduados)

Como reconstruir a marca de um país

Tariro Mzezewa apresenta algumas dicas para reconstruir a marca de um determinado país a partir da experiência da Colômbia, Ruanda e Croácia. Os três países estiveram, no passado recente, envolvidos em problemas estruturais que afastam turistas e interessados: drogas, extermínio e guerra. Para Mzezewa, não é possível esquecer o passado. Mas é possível usá-lo em uma campanha de marketing. Além disto, é importante "trazer os aviões", o que inclui melhorar as conexões aéreas, como ocorreu na Croácia. Encontrar um símbolo também é um lição importante: a Colômbia usou o fato de ter muitos pássaros. E ter sido berço de Gabriel Garcia Marquez. Ruanda apelou para os influenciadores, o que incluiu a apresentadora DeGeneres e jogadores de futebol do Arsenal. Finalmente, uma boa dose de sorte, como ocorreu com a Croácia.

O Brasil poderia apreender com estes três países para reconstruir sua marca no exterior.

Quando a amostra pode

Um artigo sobre o uso de denuncia por parte dos reguladores em valores mobiliários mostrou que estas denúncias terminam por gerar uma punição mais elevada para as empresas e funcionários envolvidos, além de prisões mais longas. Além disto, o processo no regulador é mais ágil. Assim, as denúncias são relevantes para a investigação de fraudes financeiras.

Isto foi publicado no Journal of Accounting Research, um dos melhores periódicos contábeis. Este periódico disponibilizou os dados dos autores, como é cada vez mais comum no periódicos de melhor nível.

Usando os dados, outro pesquisador, Kuvvet (2019) fez algo interessante. Como denúncias de fraudes não são eventos normais nas empresas - aparece em 20% da amostra do trabalho original - ele observou que eliminando as 11 principais empresas, ou menos de 1% da amostra, mas com maiores penalidades, o efeito obtido por Call et al no trabalho original desaparecia. Isto é bastante interessante. Kuvvet mandou sua crítica para o JAR que não publicou. Mas o argumento de Kuvvet pode ser encontrado aqui.

O assunto para este blogueiro em um comentário encaminhado à Andrew Gelman, um especialista em estatística.

´Rir é o melhor remédio

Uma pessoa normal faz e um acadêmico faz: Férias

Valor, preço e teto inicial de negociação

Embora o orçamento da União estime 16,2 bilhões de reais de arrecadação com o processo de privatização da Eletrobras , é “impossível” dizer agora qual será o valor da desestatização, disse nesta segunda-feira o ministro de Minas e Energia, Bento Albuquerque.

Ele disse ainda que não quer e não pode dizer quanto a Eletrobras vale, e o mercado também tem que esperar pela operação de privatização, prevista para o segundo semestre de 2020.

O texto é da Reuters, publicado aqui. Há uma confusão entre preço, valor e preço inicial de negociação. Provavelmente o que se quer saber é este último, já que o valor é uma opinião e depende de cada pessoa; já o preço é resultado de um mercado de compra e venda, que não é o caso. Assim, não faz sentido a questão para o ministro: quem deve se pronunciar é uma empresa contratada para determinar este preço inicial de negociação. Um ministro pode ter uma vaga ideia, mas não deveria se pronunciar.

Dicionário e-Termos

Um projeto colaborativo permite que a comunidade acadêmica possa padronizar a utilização de termos científicos. Trata-se do e-Termos e já possui pelo menos um dos trabalhos na área de sustentação ambiental.

O Projeto e-Termos, estrutura formal que suporta e abriga os trabalhos do e-Termos, é um projeto acadêmico desenvolvido em parceria entre a Embrapa Informática Agropecuária (CNPTIA), Universidade de São Paulo (USP Campus de São Carlos, SP) e Universidade Federal de São Carlos (UFSCar), representados pelos laboratórios de pesquisa LabInfo (Laboratório de Organização e Tratamento da Informação Eletrônica), NILC (Núcleo Interinstitucional de Lingüística Computacional) e o GETerm (Grupo de Estudos e Pesquisas em Terminologia), localizados nas três instituições, respectivamente.

Apoiado nas competências de cada laboratório, o Projeto e-Termos busca propor soluções para a viabilização da pesquisa e da prática terminológica, por meio da ampla utilização de um ambiente computacional colaborativo baseado na Web. Resumidamente, como proposta de pesquisa, os principais objetivos deste projeto são: 1) a criação e implementação do e-Termos (ambiente web) e 2) posteriormente a avaliação do seu uso colaborativo na prática terminológica.

Este projeto tem a cooperação de vários profissionais, autônomos, professores, bolsistas e alunos de graduação e pós-graduação das instituiçõs supracitadas, bem como colaboradores de várias outras instituições de ensino e pesquisa, que contribuem direta e indiretamente para o seu sucesso

Eleições na Bolívia

A pesquisa sobre fraude em eleições usa muito instrumento da auditoria. E vice-versa.

Recentemente, a Bolívia teve uma votação presidencial, onde o então presidente foi declarado vencedor. Protestos reclamavam que ocorreu fraude na votação. Um texto (via aqui) indica que provavelmente não ocorreu fraude na eleição:

The TSE has two vote-counting systems. The first is a quick count known as the Transmisión de Resultados Electorales Preliminares (TREP, hereafter referred to as the quick count). This is a system that Bolivia and several other Latin American countries have implemented following OAS recommendations. . . . and is designed to deliver a swift — but incomplete and not definitive — result on the night of the elections to give the media an indication of the voting tendency and to inform the public. The TSE is unlikely to process 100 percent of the results in the quick count in nationwide votes due to logistical limitations and the amount processed can vary widely by geography and the type of ballot. . . .

The second vote-counting system is the official count (or cómputo), which is legally binding under Bolivian law. The official count is more thorough and precise and takes longer. It is the only valid vote tallying system, and the TSE uses it to determine and announce the final election results. . . .

In these elections, the results of the official count generally coincided with those of the quick count, which ended once 95.63 percent of tally sheets were counted, with Morales having a lead of 46.86 percent to Mesa’s 36.72. The final official count, with 100 percent of votes counted, resulted in Morales winning the election in the first round with 47.08 percent, to Mesa’s 36.51 percent.

Ou seja, as duas contagens (a rápida e a oficial) apresentaram resultados convergentes. Mais ainda, não ocorreu interrupção na contagem, que seria um sinal de fraude. O gráfico mostra uma evolução consistente:

Mas o relatório da OAS discorda:

Given all the irregularities observed, it is impossible to guarantee the integrity of the data and certify the accuracy of the results. (...) It should be borne in mind that the irregularities we have pointed out are those we observed in a short period of time. It is also important to point out that it was not possible to analyze the original tally sheets for the departments of Potosí, Chuquisaca, and Santa Cruz as part of the documentation had been burned. In all likelihood, given more time to process documentation, even more irregularities would surface.

Rir é o melhor remédio

pensando muito em contabilidade

Efeitos do Protecionismo de Trump

Resumo:

After decades of supporting free trade, in 2018 the U.S. raised import tariffs and major trade partners retaliated. We analyze the short-run impact of this return to protectionism on the U.S. economy. Import and retaliatory tariffs caused large declines in imports and exports. Prices of imports targeted by tariffs did not fall, implying complete pass-through of tariffs to duty-inclusive prices. The resulting losses to U.S. consumers and firms who buy imports was $51 billion, or 0.27% of GDP. We embed the estimated trade elasticities in a general-equilibrium model of the U.S. economy. After accounting for tariff revenue and gains to domestic producers, the aggregate real income loss was $7.2 billion, or 0.04% of GDP. Import tariffs favored sectors concentrated in politically competitive counties, and the model implies that tradeable-sector workers in heavily Republican counties were the most negatively affected due to the retaliatory tariffs.

The Return to Protectionism
Pablo D Fajgelbaum, Pinelopi K Goldberg, Patrick J Kennedy, Amit K Khandelwal
The Quarterly Journal of Economics, qjz036, https://doi.org/10.1093/qje/qjz036

Formato Eletrônico das IFRS na Europa

A Europa está adotando o formato eletrônico das demonstrações contábeis, tendo por base as IFRS, a parte de 2020. Em 2014, o Iasb constituiu um grupo de trabalho para elaborar um guia com esta finalidade. Há alguns meses, a European Securities and Markets Authorities aprovou o European Single Eletronic Format. Por enquanto, as mudanças não alcançam as notas explicativas; somente em 2022 é que terá esta abrangência.

A finalidade é a comparabilidade das informações e facilitar o acesso às demonstrações.

Leia mais aqui

Custos ocultos do Uber

O pesquisador Ken Jacobs, da Universidade da Califórnia em Berkeley, nos Estados Unidos, estudou os custos ocultos com os quais motoristas da Uber têm de lidar. Jacobs os dividiu em cinco áreas principais: o tempo gasto esperando viagens, o custo de retornar às áreas mais concorridas após uma viagem, a manutenção e seguro de veículos, a falta de remuneração quando se fica doente, durante os intervalos para almoço e horas livres, e a não remuneração das férias. "Tende-se a subestimar as despesas reais de um motorista", diz Jacobs.

Meera Joshi, ex-chefe da Comissão de Táxis e Limusines de Nova York, responsável por regular serviços como o Uber em toda a cidade, diz que dados mais precisos são essenciais. (...) "O que descobrimos foi que as condições eram piores do que os motoristas nos descreveram, e 96% ganhavam menos que o salário mínimo na cidade. A maioria dos motoristas era a principal fonte de renda de suas famílias", acrescenta. (...)

O estudo da Universidade Oxford também destaca que os motoristas da Uber têm níveis mais altos de satisfação com a vida que outros trabalhadores, mas também níveis mais altos de ansiedade. "É o paradoxo do Uber", diz Duncan McCann, pesquisador da New Economics Foundation. "É uma prisão e algo libertador. Você pode ativar o aplicativo e começar a trabalhar, mas, se você tem uma família para sustentar, é obviamente menos flexível. Você precisa trabalhar quando há mais demanda: horários de pico e fins de semana."

Leia mais aqui

Uber banida de Londres

Para ser motorista de táxi em Londres é necessário passar por um exame rigoroso. Para ser aprovado, o motorista deve saber as ruas da cidade sem precisar consultar um livro ou aplicativo.

Os populares aplicativos seriam uma ameaça para este tipo de serviço. Mas agora, a entidade que regula os transportes em Londres não emitiu uma nova licença para que o Uber fosse aprovados como operador de transporte. Em outras palavras, a Uber está impedida de operar em Londres. Mas a empresa deve apelar e continuar com as operações de maneira provisória.

O motivo da recusa foi "segurança". O regulador diz que a empresa permite veículos com motoristas sem licença e sem seguro.

Rir é o melhor remédio

Trabalho em casa ou no escritório

Análise Fundamentalista está em extinção

O espaço da análise fundamentalista será cada vez menor num mercado dominado por métodos matemáticos e computacionais:

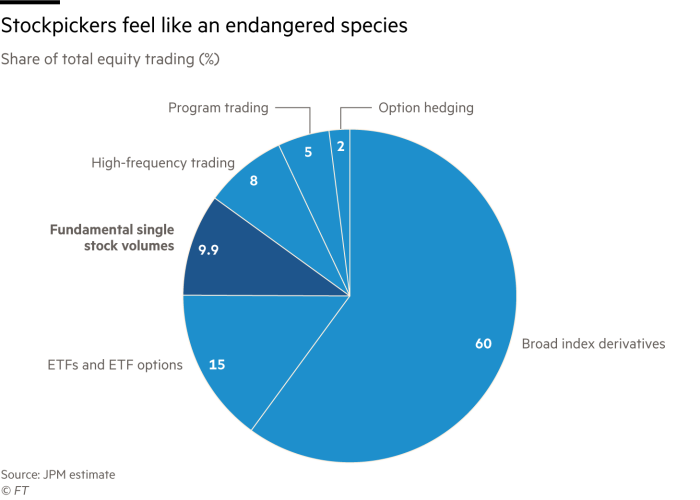
In late 2013, academics at computer-driven funds giant AQR posted online a research paper called “Buffett’s Alpha.” The paper argued that the returns of the legendary investor could largely be explained by buying stocks that were cheap, safe and high quality — and then using debt to juice returns. The implications were potentially huge. For all the mystique surrounding the investing strategy of the Sage of Omaha, much of it could apparently be replicated by a machine scanning the market for stocks displaying such characteristics. AQR launched a fund that applied this approach to a large basket of global equities. Other quant firms are joining in; London-based start-up Havelock is currently trying to fashion an algorithm that mimics Mr Buffett. Such attempts are helping to undermine what was once a prominent feature of the investing landscape: the cult of the star stock picker.

Also threatening these vaunted operators has been the decade-long equities bull market, fuelled by trillions of dollars of central bank asset purchases, which has boosted the appeal of cheap index-tracking funds. Spotting out-of-favour bargain stocks has been a duff strategy compared with buying and holding stocks already on a roll, or fast-growing technology firms. As a result, many of the former stars have been left looking decidedly ordinary. “Stock pickers just haven’t performed and that’s why investors are pulling out of active managers,” said Kevin Arenson, chief investment officer at Stenham Asset Management, which invests in hedge funds.

Fonte: aqui